In this article, I want to discuss how the intersection area of two circles can be calculated. Given are only the two circles with their corresponding centre point together with the radius and the result is the area which both circles share in common. First, I want to take a look at how the intersection area can be calculated and then how the needed variables are derived from the given data. At the end of the article, I supply running code in C++.
The following figure illustrates the general problem. A small and a large circle is shown and both share a common area at the right part of the first circle.
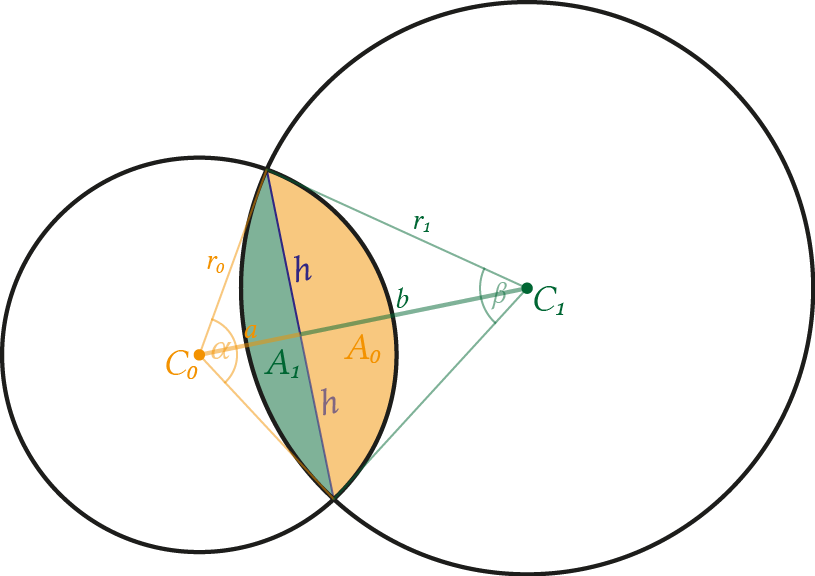
As the figure already depicts, the problem is solved by calculating the area of the two circular segments formed by the two circles. The total intersecting area is then simply
\begin{equation*} A_0 + A_1. \end{equation*}As equation 15 from MathWorld shows, the area of one circular segment is calculated as (all angles are in radiant)
\begin{equation*} \begin{split} A &= \frac{1}{2} r^2 (\theta - \sin(\theta)), \\ &= \frac{1}{2} r^2 \theta - \frac{1}{2} r^2 \sin(\theta). \end{split} \end{equation*}The formula consists of two parts. The left part is the formula for the area of the circular sector (complete wedge limited by the radius), which is similar to the formula of the complete circle area (\( r^2\pi \)) where the arc length takes a complete round of the circle. Here instead, the arc length is explicitly specified by \(\theta\) instead of \(\pi\). If you plug a complete round into \(\theta\), you get the same result: \( \frac{1}{2} r^2 2\pi = r^2\pi \). The right part calculates the area of the isosceles triangle (triangle with the radii as sides and heights as baseline), which is a little bit harder to see. With the double-angle formula
\begin{equation*} \sin(2x) = 2\sin(x)\cos(y) \end{equation*}\(\sin(\theta)\) can be rewritten as
\begin{equation*} \sin(\theta) = 2\sin\left(\frac{1}{2}\theta\right) \cos\left(\frac{1}{2}\theta\right). \end{equation*}This leaves for the right part of the above formula
\begin{equation*} \frac{1}{2} r^2 \sin(\theta) = r^2 \sin\left(\frac{1}{2}\theta\right) \cos\left(\frac{1}{2}\theta\right). \end{equation*}Also, note that \(r \sin\left(\frac{1}{2}\theta\right) = a\) and \( r \cos\left(\frac{1}{2}\theta\right) = h\) (imagine the angle \(\frac{\alpha}{2}\) from the above figure in a unit circle), which results in
\begin{equation*} r^2 \sin\left(\frac{1}{2}\theta\right) \cos\left(\frac{1}{2}\theta\right) = ar \end{equation*}and since we have an isosceles triangle, this is exactly the area of the triangle.
Originally, the formula is only defined for angles \(\theta < \pi\) (and probably \(\theta \geq 0\)). In this case, \(\sin(\theta)\) is non-negative and the area of the circular segment is the subtraction of the triangle area from the circular sector area (\( A = A_{sector} - A_{triangle} \)). But as far as I can see, this formula also works for \(\theta \geq \pi\), if the angle stays in the range \([0;2\pi]\). In this case, the triangle area and the area of the circular sector need to get added up (\( A = A_{sector} + A_{triangle} \)), which is considered in the formula by a negative \(\sin(\theta)\) (note the negative factor before the \(\sin(\theta)\) function). The next figure also depicts this situation.
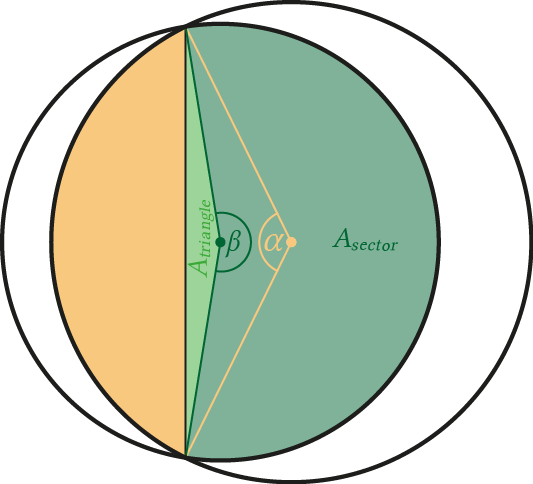
The following table gives a small example of these two elementary cases (circular sector for one circle).
| \(r\) | \(\theta\) | \(a = \frac{1}{2} r^2 \theta\) | \(b = \frac{1}{2} r^2 \sin(\theta)\) | \(A = a - b\) |
|---|---|---|---|---|
| \(2\) | \(\frac{\pi}{3} = 60°\) | \(\frac{2 \pi }{3}\) | \(\sqrt{3}\) | \(\frac{2 \pi }{3} - \sqrt{3} = 0.362344\) |
| \(2\) | \(\frac{4\pi}{3} = 240°\) | \(\frac{8 \pi }{3}\) | \(-\sqrt{3}\) | \(\frac{8 \pi }{3}- (-\sqrt{3}) = 10.1096\) |
It is also from interest to see the area of the circular segment as a function of \(\theta\):
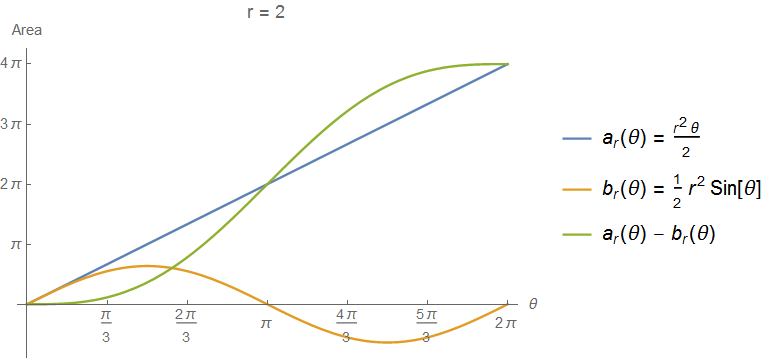
It is noticeable that the area of one circular segment (green line) starts degressively from the case where the two circles just touch each other, because here the area of the triangle is subtracted. Beginning from the middle at \(\theta = \pi\) the area of the triangle gets added and the green line proceeds progressively until the two circles contain each other completely (full circle area \(2^2\pi=4\pi\)). Of course, the function itself is independent of any intersecting scenario (it gives just the area for a circular segment), but the interpretation fits to our intersecting problem (remember that in total areas of two circular segments will get added up).
Next, we want to use the formula. The radius \(r\) of the circle is known, but we need to calculate the angle \(\theta\). Let's start with the first circle. The second then follows easily. With the notation from the figure, we need the angle \(\alpha\). Using trigonometric functions, this can be done by
\begin{equation*} \begin{split} \tan{\frac{\alpha}{2}} &= \frac{\text{opposite}}{\text{adjacent}} = \frac{h}{a} \\ \text{atan2}(y, x) &= \text{atan2}(h, a) = \frac{\alpha}{2} \end{split} \end{equation*}The \(\text{atan2}(y, x)\) function is the extended version of the \(\tan^{-1}(x)\) function where the sign of the two arguments is used to determine a resulting angle in the range \([-\pi;\pi]\). Please note that the \(y\) argument is passed first. This is common in many implementations, like also in the here used version of the C++ standard library std::atan2(double y, double x). For the intersection area the angle should be be positive and in the range \([0;2\pi]\) as discussed before, so in total we have
Firstly, the range is expanded to \([-2\pi;2\pi]\) (factor from the previous equation, since the height \(h\) covers only half of the triangle). Secondly, positivity is ensured by adding \(+2\pi\) leaving a resulting interval of \([0;4\pi]\). Thirdly, the interval is shrinked to \([0;2\pi]\) to stay inside one circle round.
Before we can calculate the \(\alpha\) angle, we need to find \(a\) and \(h\)1. Let's start with \(a\). The two circles build two triangles (not to be confused with the previous triangle used to calculate the area of the circular segment) with the total baseline \(d=a+b = \left\| C_0 - C_1 \right\|_2 \) and the radii (\(r_0,r_1\)) as sides, which give us two equations
\begin{equation*} \begin{split} r_0^2 &= a^2 + h^2, \\ r_1^2 &= b^2 + h^2. \end{split} \end{equation*}The parameter \(b\) in the second equation can be omitted (using \(d-a=b\))
\begin{equation*} r_1^2 = b^2 + h^2 = (d-a)^2 + h^2 = d^2 - 2da + a^2 + h^2 \end{equation*}and the equation solved by \(h^2\)
\begin{equation*} h^2 = r_1^2 - d^2 + 2da - a^2. \end{equation*}Plugging this into the equation for the first triangle
\begin{equation*} \begin{split} r_0^2 &= a^2 + r_1^2 - d^2 + 2da - a^2 \\ r_0^2 - r_1^2 + d^2 &= 2da \\ a &= \frac{r_0^2 - r_1^2 + d^2}{2d} \end{split} \end{equation*}results in the desired distance \(a\). This directly gives us the height
\begin{equation*} h = \sqrt{r_0^2 - a^2}. \end{equation*}Using the existing information the angle \(\beta\) for the second circle can now easily be calculated
\begin{equation*} \beta = \text{atan2}(h, d-a) \cdot 2 + 2 \pi \mod 2 \pi. \end{equation*}Now we have every parameter we need to use the area function and it is time to summarize the findings in some code.
/**
* @brief Calculates the intersection area of two circles.
*
* @param center0 center point of the first circle
* @param radius0 radius of the first circle
* @param center1 center point of the second circle
* @param radius1 radius of the second circle
* @return intersection area (normally in px²)
*/
double intersectionAreaCircles(const cv::Point2d& center0, const double radius0, const cv::Point2d& center1, const double radius1)
{
CV_Assert(radius0 >= 0 && radius1 >= 0);
const double d_distance = cv::norm(center0 - center1); // Euclidean distance between the two center points
if (d_distance > radius0 + radius1)
{
/* Circles do not intersect */
return 0.0;
}
if (d_distance <= fabs(radius0 - radius1)) // <= instead of <, because when the circles touch each other, it should be treated as inside
{
/* One circle is contained completely inside the other, just return the smaller circle area */
const double A0 = PI * std::pow(radius0, 2);
const double A1 = PI * std::pow(radius1, 2);
return radius0 < radius1 ? A0 : A1;
}
if (d_distance == 0.0 && radius0 == radius1)
{
/* Both circles are equal, just return the circle area */
return PI * std::pow(radius0, 2);
}
/* Calculate distances */
const double a_distanceCenterFirst = (std::pow(radius0, 2) - std::pow(radius1, 2) + std::pow(d_distance, 2)) / (2 * d_distance); // First center point to the middle line
const double b_distanceCenterSecond = d_distance - a_distanceCenterFirst; // Second centre point to the middle line
const double h_height = std::sqrt(std::pow(radius0, 2) - std::pow(a_distanceCenterFirst, 2)); // Half of the middle line
/* Calculate angles */
const double alpha = std::fmod(std::atan2(h_height, a_distanceCenterFirst) * 2.0 + 2 * PI, 2 * PI); // Central angle for the first circle
const double beta = std::fmod(std::atan2(h_height, b_distanceCenterSecond) * 2.0 + 2 * PI, 2 * PI); // Central angle for the second circle
/* Calculate areas */
const double A0 = std::pow(radius0, 2) / 2.0 * (alpha - std::sin(alpha)); // Area of the first circula segment
const double A1 = std::pow(radius1, 2) / 2.0 * (beta - std::sin(beta)); // Area of the second circula segment
return A0 + A1;
}
Basically, the code is a direct implementation of the discussed points. The treatment of the three special cases (no intersection, circles completely inside each other, equal circles) are also from Paul Bourke's statements. Beside the functions of the C++ standard library I also use some OpenCV datatypes (the code is from a project which uses this library). But they play no important role here, so you can easily replace them with your own data structures.
I also have a small test method which covers four basic cases. The reference values are calculated in a Mathematica notebook.
void testIntersectionAreaCircles()
{
/* Reference values from IntersectingCirclesArea_TestCases.nb */
const double accuracy = 0.00001;
CV_Assert(std::fabs(intersectionAreaCircles(cv::Point2d(200, 200), 100, cv::Point2d(300, 200), 120) - 16623.07332) < accuracy); // Normal intersection
CV_Assert(std::fabs(intersectionAreaCircles(cv::Point2d(200, 200), 100, cv::Point2d(220, 200), 120) - 31415.92654) < accuracy); // Touch, inside
CV_Assert(std::fabs(intersectionAreaCircles(cv::Point2d(200, 200), 100, cv::Point2d(400, 200), 100) - 0.0) < accuracy); // Touch, outside
CV_Assert(std::fabs(intersectionAreaCircles(cv::Point2d(180, 200), 100, cv::Point2d(220, 200), 120) - 28434.24854) < accuracy); // Angle greater than 180°
}
List of attached files:
- IntersectingCirclesArea.nb [PDF] (Mathematica notebook with the figure of the area of the circular sector)
- IntersectingCirclesArea_TestCases.nb [PDF] (Mathematica notebook to calculate the reference values used in the test method)